Behov for ny teknologi
Byggesteienene i dagens datamaskiner kalles transistorer, og vi pleide å gjøre datamaskinene raskere på to måter: ved å gjøre transistorene mindre og ved å øke hvor raskt vi skrur dem av og på. I dag klarer vi bare det første.
Hvor fort transitorene blir skrudd av og på er gitt ved prossesorens klokkefrekvens. Dersom du levde rundt årtusenskiftet husker du kanskje en tid hvor denne klokkefrekvensen økte drastisk fra år til år. Dette er ikke lenger tilfellet, og idag har klokkefrekvensen stagnert ved rundt 2-3 GHz. For å kompensere for denne stagnasjonen begynte vi å legge til flere prosessorkjerner, men ikke alle problemer kan løses ved å legge til flere kjerner.
Utfordringer med transistorer
Transistorstørrelsen, derimot, har fortsatt med å bli mindre og mindre, men heller ikke denne utviklingen kan vare for alltid. Det blir vanskeligere og vanskeligere å lage mindre transistorer, og det er grunn til å tro at denne utviklingen begynner å nærme seg slutten. Dette er blant annet fordi transistorene har blitt så små at kvantemekanikk spiller en viktig rolle. Kvantemekanikk er nødvendig for å forstå verden på liten skala, og nå som transistorene bare er noen få nanometer store blir kvantemekaniske effekter stadig viktigere. Dermed blir prosessen med å forminske transistorene stadig vanskeligere.
Et eksempel på en slik kvantemekanisk effekt er tunnelering, som er at elektroner kan gå gjennom vegger som man fra klassisk fysikk skulle trodd var umulig, så lenge disse veggene er tynne nok. Hele poenget med transistorer er at de skal fungere som vegger som kan skrus av og på. Hvis elektronene kan tunnelere gjennom så fungerer transistorene dårlig.
Kanskje enda viktigere enn å gjøre datamaskinene raskere er det å gjøre de mer energieffektive. En stadig økende del av verdens energibudsjett går til datamaskiner, enten det er til store datasentre hos Amazon eller Google eller bitcoin-mining [1]. Å finne et energieffektivt alternativ til datamaskinteknologi er dermed ikke bare et teknologisk problem, men også et økonomisk og klimarelevant problem.
Dette er altså motivasjonen bak det vi jobber med på senteret for kvante-spinntronikk (QuSpin), et såkalt “senter for fremragende forskning” på NTNU [2].
Kvantefysikk på nanoskalaen
Alternativet vi jobber med på QuSpin er spinntronikk. Spinntronikk handler om å manipulere spinn istedenfor elektrisk ladning, og dette har potensialet til å være mye mer energieffektivt.
Spinn er en kvantemekanisk egenskap som gjør at elektroner er som bittesmå magneter. Elektroner spinner alltid like mye, men retningen kan variere, og man kan endre retningen ved for eksempel å bruke magnetfelt. Kort fortalt og litt forenklet kan spinntronikk oppsummeres med at man kan sende informasjon ved å flippe elektroner heller enn å flytte på dem, og dette kan være mye mer energieffektivt.
Når det er sagt så jobber vi ikke faktisk med å lage datakomponenter med spinntronikk på QuSpin. Vi jobber med å forstå fysikken som trengs for å kunne bruke spinntronikk i fremtidens datamaskiner. Vi driver med såkalt grunnforskning.
Kvantemekanikk på nanoskalaen er ganske komplisert, siden det er massevis av vekselvirkende komponenter, og det er denne skalaen som er relevant for spinntronikk og fremtidens datamaskiner spesielt.
Superledning og tidsavhengighet
Personlig jobber jeg typisk med å utforske hybridsystemer som involverer superledere [3]. Det betyr at jeg ser på systemer som er satt sammen av flere typer materialer med forskjellige egenskaper, og superledning er ofte en del av bildet. En av egenskapene til superledere er at de kan sende strøm uten noe tap av energi, og derfor hadde det vært fint å kunne involvere dem i fremtidens energieffektive maskiner.
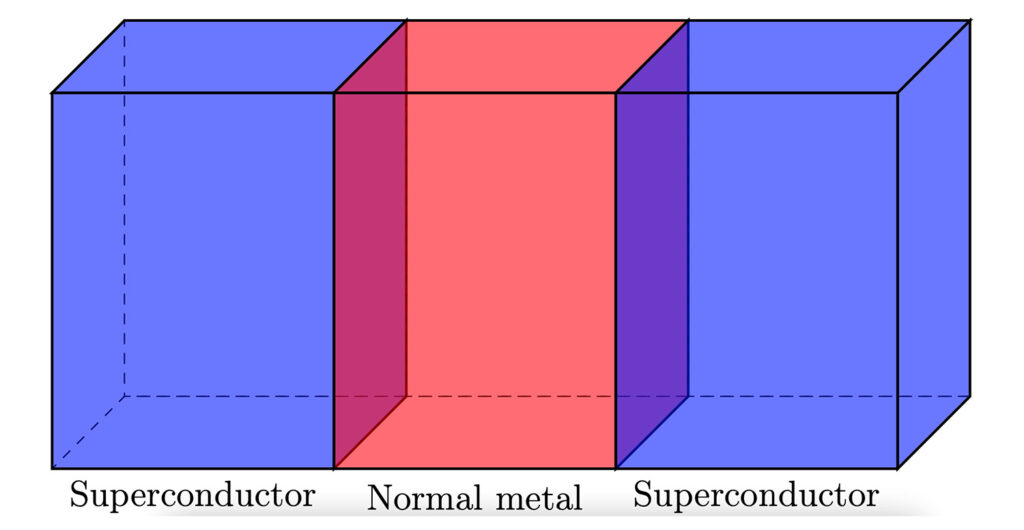
Grunnen til at hybridstrukturer er så interessant er at man kan få helt ny oppførsel ved å kombinere forskjellige typer materialer. For eksempel, vanlig superledning kan ikke brukes til å sende spinnstrøm, så selv om superledere kan sende vanlig elektrisk strøm uten motstand så er de i utgangspunktet tilsynelatende ubrukelige til spinntronikk. Dersom du kombinerer den med en magnet, derimot, vil du kunne få en ny type superledning, såkalt spinn-triplet superledning, noe som kan sende spinnstrøm uten energitap.

En viktig del av spørsmålet om hvordan nanostrukturer fungerer, er hvordan de utvikler seg i tid. Dette spørsmålet har lenge vært vanskelig når det kommer til systemer som involverer superledning. Dette er fordi disse systemene typisk studeres med en differensiallikning som kalles Usadel-likningen, og denne er mye mer komplisert når systemet utvikler seg i tid.
Uten tidsavhengighet er likningen fortsatt komplisert, men den er i det minste av en type som vi vet hvordan vi kan få datamaskiner til å løse. Vi har algoritmer, slik som elementmetoden [4], som gjør at vi kan løse likninger på datamaskiner selv om det er umulig å løse dem for hånd. Det som gjør tidsavhengighet i Usadel-likningen spesielt vanskelig er at den inneholder ledd som ikke kan puttes inn i disse algoritmene. Den har noen kompliserte derivasjonsoperatorer av uendelig orden. Dette gjør at den ikke kan løses, selv på datamaskin.
Nye resultater åpner nye dører
Da jeg begynte på min doktorgrad var ett av målene å bidra til å gjøre det mer overkommelig å studere tidsavhengige systemer. Det var allerede et par tilfeller hvor tidsavhengighet var mulig å løse. Dersom ting endret seg veldig sakte eller periodisk, slik som en pendel som går frem og tilbake med fast frekvens, så kunne likningene skrives om til noe som var mulig å løse. Mange fysisk relevante systemer er imidlertid ikke av den typen. For eksempel, som nevnt over så skrus transistorene i en datamaskin seg av og på milliarder av ganger i sekundet. Dette er verken sakte eller periodisk. Dersom vi ønsker at systemene vi studerer skal være relevant for fremtidens datamaskiner så bør vi dermed vite hvordan de oppfører seg når de endrer seg raskt og ikke-periodisk.
På et tidspunkt slo det meg at Usadel-likningen kunne løses med vilkårlig tidsavhengighet dersom man gjorde en relativt grei antagelse om egenskapene til systemet.
Detaljene kan sees i publikasjonen som er henvist til i referanselisten under [5]. I praksis betyr dette at Usadel-likningen nå kan løses uavhengig av hva slags tidsavhengighet det er snakk om.
For å teste ut denne nye metoden så vi på hva som skjer med en av de vanligste hybridstrukturene dersom man skrur på magnetfelt [5]. Spinntronikk handler om å utnytte at elektroner er bittesmå magneter. Det betyr at å endre magnetfeltet er spesielt relevant i spinntronikksammenheng.
Det er velkjent hva som skjer uten tidsavhengighet: du dreper superledningen ved å sette på et magnetfelt. Dermed vet vi at så lenge vi venter lenge nok så vil superledningen etterhvert bli ødelagt. Men hva skjer i overgangen? Det viser seg at rett etter du har skrudd på magnetfeltet så kan superledningen faktisk bli dramatisk forsterket. Dette var ganske overaskende fordi det er helt motsatt av hva man skulle forvente fra hvordan situasjonen ser ut i det statiske tilfellet.
Dette er eksempel på hvor viktig det er å kunne løse de tidsavhengige likningene for å kunne forstå hva som skjer. Overraskende ting kan skje når du lar det endre seg i tid, og det er viktig å vite om dette før man eventuelt bruker det i ny teknologi slik som fremtidens datamaskiner. Det blir spennende å se hvilke andre ting vi kan finne ut av nå som vi kan se på vilkårlige tidsavhengige systemer.
Referanseliste
[1] N. Jones, How to stop data centers from gobbling up the world’s electricity, Nature 561, 163-166 (2018)
[3] Litt om kvantefysikken bak superledning for de spesielt interesserte:
Vi skiller mellom to typer partikler: bosoner (fotoner, helium osv) og fermioner (elektroner osv). Forskjellen er at det er umulig å få to fermioner inn i samme kvantemekaniske tilstand, mens bosoner kan godt være i samme tilstand. Det betyr at du kan ha så mange bosoner du vil i samme posisjon, for eksempel. Faktisk har det seg sånn at dersom du har en stor samling av bosoner og senker temperaturen nok, så kan alle bosonene havne i samme tilstand. Du kan ha alle de feks 1023 bosonene i samme kvantemekaniske tilstand. Da får man en slags makroskopisk kvantemekanisk bølgefunksjon. Man hører innimellom at kvantemekanikk bare er relevant for bittesmå ting, men dette er altså et eksempel på kvantemekanikk på en mer daglidags skala. Dette er mekanismen bak superledning og også superfluider og det som kalles Bose-Einstein kondensat.
En av de mest fantastiske tingene vi mennesker har funnet ut av er at det er en dyp sammenheng mellom partkkelers spinn og skillet mellom boson og fermion. Som jeg nevnte over så spinner elektroner alltid like mye, selv om retningen kan variere.
Vi sier at elektroner har spinn lik ½. Fotoner har derimot spinn lik 1. Den dype sammenhengen (som går under navnet spinn–statistikk-teoremet) er at alt som har et heltall spinn er bosoner mens det som har et heltall + ½ er fermioner. Det betyr at elektroner, som har spinn ½, er fermioner. Her kommer det viktige spørsmålet: hva med to elektroner? Dersom du ser på en samling av 2 elektroner så vil de til sammen ha spinn enten 0 (dersom spinnene peker i motsatt retning) eller 1 (dersom de peker i samme retning). I begge tilfeller er det totale spinnet lik et heltall, som betyr at elektronpar er bosoner. Tilsvarende er heliumatomer også bosoner, fordi de er lagd av et partall antall fermioner.
Det som skjer når et metall blir en superleder er altså at når du senker temperaturen lavt nok så danner en del av elektronene par som tilsammen blir bosoner. Disse kalles Cooper-par. Disse bosonene kan være i samme kvantemekaniske tilstand, og ved lav temperatur vil de faktisk helst være i samme tilstand. Dette gjør at du får superledning: et makroskopisk kvantemekanisk fenomen med en rekke utrolige egenskaper, slik som strøm uten energitap og levitasjon på togskinner av magneter (se feks denne videoen på YouTube om QuantumLevitation).
[4] Elementmetoden er bare en av mange mulige algoritmer, men det er den jeg typisk bruker. Den engelske wikipediasiden er tilgjengelig for «Finite element method», og en vitenskapelig artikkel som viser hvordan den kan brukes til å løse Usadel-likningen (M. Amundsen, J. Linder, General solution of 2D and 3D superconducting quasiclassical systems: coalescing vortices and nanoisland geometries. Sci. Rep. 6, 22765
[5] E. H. Fyhn og J. Linder, Temporarily enhanced superconductivity from magnetic fields, Phys. Rev. B 103, L100502 (2021). Tilgjengelig preprint (PDF)


